AVERAGE関数(平均値)にはある欠点が潜んでいます。
その欠点を補うために、「MEDIAN」と「STDEV.P」の2つの関数をあわせて使いましょう、というお話です。
平均値ばかりを見ていると見誤る。
なにかしら収集したデータについて、その「平均値」を求めようとする場合。ExcelのAVERAGE関数を使って「平均値を計算する」ということがあるでしょう。
たとえば。飲食店のオーナーが、「日々の売上高の平均を知りたいぞ!」みたいな。
そんなときに、ExcelでAVERAGE関数を使って計算することはカンタンですが。あわせて使うべき2つの関数があります。
つまり、AVERAGE関数だけではチカラ不足だ、ということです。
結論として。AVERAGE関数といっしょに、「MEDIAN」と「STDEV.P」の2つの関数を使うこと。これにより、AVERAGE関数(平均値)に潜む「欠点」を補うことができます。
AVERAGE関数の欠点? と思われるかもですが。
その疑問への答えと、それぞれの関数の「使い方」や「見方」についてお話をしていきます ↓
- AVERAGE関数の使い方
- MEDIAN関数の使い方と見方(AVERAGE関数の欠点その1)
- STDEV.P関数の使い方と見方(AVERAGE関数の欠点その2)
それでは、このあと順番に見ていきましょう。
AVERAGE関数の使い方
MEDIANとSTDEV.Pのお話をする前に。まずは、AVERAGE関数の使い方を確認しておきましょう。
具体例として、とある飲食店の平日ランチの売上高データ(単位は円)を使います ↓
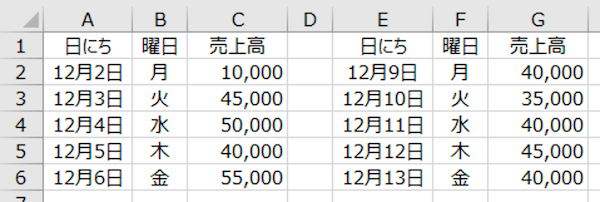
上記のとおり、「12月2日(月)〜12月6日(金)」までの5日間と、「12月9日(月)〜12月10日(金)」までの5日間とのデータがあります。
それぞれの5日間について、日々のランチ売上高の平均値を計算してみましょう。というときに使うのが「AVERAGE関数」です。
使い方はカンタン。任意のセルに次の算式を入力するだけです ↓
= AVERAGE(範囲)
算式中の「範囲」には、「12月2日(月)〜12月6日(金)」までの5日間であれば「C2からC6」のセル、「12月9日(月)〜12月10日(金)」までの5日間であれば「G2からG6」のセルになります。
実際に入力してみると、こんな感じです ↓
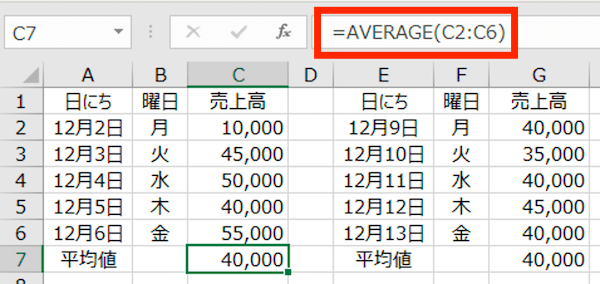
上記のとおり、C7のセルに「=AVERAGE(C2:C6)」と入力しています(算式は赤枠内を参照)。
これにより計算されたC7のセルの値 40,000円が、「12月2日(月)〜12月6日(金)」までの5日間のランチ売上高の平均値です。
同じようにして、「12月9日(月)〜12月10日(金)」までの5日間も計算してみると、奇遇にも平均値は同じ 40,000円でした。
これだけ(平均値だけ)を見ていると、日々の平均ランチ売上高 40,000円という「同じ5日間」に見えなくもないわけですが。
実は「似て非なる5日間」であることがわからない… というのが、AVERAGE関数が抱える欠点になります。では、その欠点とは? を知るために、次のMEDIAN関数の話に移ることにしましょう。
MEDIAN関数の使い方と見方(AVERAGE関数の欠点その1)
AVERAGE関数が抱える欠点を補うために、まずは「MEDIAN関数」を使うことにします。そのMEDIAN関数とは、データのなかから「中央値」を計算する関数です。
中央値とは、データを小さい順(あるいは大きい順)に並べたときに、ちょうど真ん中にあるデータの値のこと。ちなみに、データの個数が偶数であれば、真ん中の2つのデータの平均値になります。
そんな中央値を計算するMEDIAN関数も、使い方はカンタン。任意のセルに次の算式を入力するだけです ↓
= MEDIAN(範囲)
さきほどの具体例を使って、実際に入力してみるとこんな感じです ↓
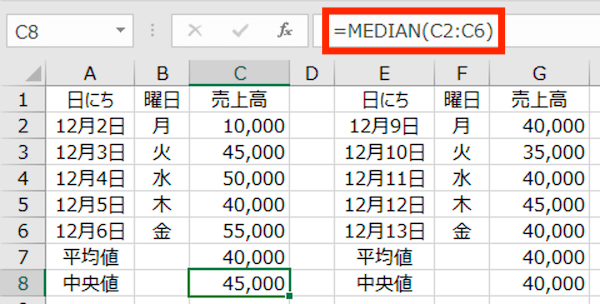
上記のとおり、C8のセルに「=MEDIAN(C2:C6)」と入力しています(算式は赤枠内を参照)。
これにより計算されたC8のセルの値 45,000円が、「12月2日(月)〜12月6日(金)」までの5日間のランチ売上高の中央値です。
同じようにして、「12月9日(月)〜12月10日(金)」までの5日間も計算してみると、中央値は 40,000円でした。
ここが、「?」と感じるべきポイントです。
さきほど見たとおり、どちらの5日間も「平均値は同じ」だったはずなのに。中央値には 5,000円の差があります。
「12月2日(月)〜12月6日(金)」までの5日間のほうが中央値が 5,000円も大きいのはなぜか?
それは、12月2日(月)を除いた4日間は、おおむね平均値を上回っているからです。言い換えると、12月2日(月)の 10,000円という極端に低い売上高が、平均値を引き下げる方向に引っ張っている、ということです。
このように、極端に低いデータ(あるいは高いデータ)を「外れ値(はずれち)」と呼びます。外れ値があると、平均値をその方向に引っ張ってしまう。
その影響は平均値を見ているだけではわからない、というのが平均値に潜む欠点になります。
具体例で言えば、12月2日(月)の 10,000円を除けば、「12月2日(月)〜12月6日(金)」の5日間のほうが、「12月9日(月)〜12月10日(金)」の5日間よりも実は好調なのです。
この場合、12月2日(月)が 10,000円と低い原因を追求すると同時に、「12月9日(月)〜12月10日(金)」が前週に比べて減少傾向である原因も追求する必要があります。
具体例ではデータ数が少ないので、ぱっと見るだけでも「外れ値」の存在に気がつくかもしれませんが。データ数が多い場合の平均値については「外れ値」を見落としてしまうかもしれません。
その場合に、平均値だけを見ていると、「平均値が外れ値の影響を受けている」ことを見落とします。そこは、AVERAGE関数とMEDIAN関数とをあわせて使うことでカバーしましょう。
STDEV.P関数の使い方と見方(AVERAGE関数の欠点その2)
AVERAGE関数が抱える欠点を補うために、「MEDIAN関数」のお話をしました。AVERAGE関数が抱える欠点はまだあります。
それを説明するために、次にお話をするのが「STDEV.P関数」です。STDEV.Pは「スタンダード・ディビエーション・ポピュレーション」の略で、日本語にすると「標準偏差」を意味します。
標準偏差とは、端的に言えば「データのバラツキ度合い」をあらわす値です。
文字で説明をするよりも、具体例で見ることにしましょう。さきほどまでの具体例とは数値が変わっていますのでご注意を ↓
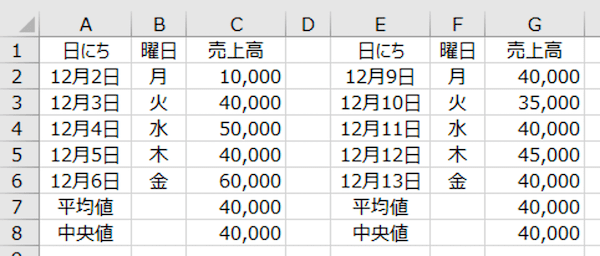
上記のとおり、「12月2日(月)〜12月6日(金)」の5日間と、「12月9日(月)〜12月10日(金)」の5日間のデータについて、それぞれ「平均値」と「中央値」を計算しています。
結果、どちらの5日間も、平均値と中央値ともにまったく同じです。ここに、標準偏差の値を加えてみましょう。
と言っても。標準偏差を計算するSTDEV.P関数も、使い方はカンタン。任意のセルに次の算式を入力するだけです ↓
= STDEV.P(範囲)
実際に入力してみると、こんな感じです ↓
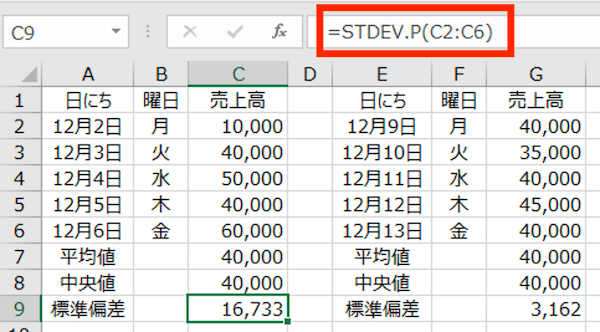
上記のとおり、C9のセルに「=STDEV.P(C2:C6)」と入力しています(算式は赤枠内を参照)。
これにより計算されたC9のセルの値 16,733円が、「12月2日(月)〜12月6日(金)」までの5日間の標準偏差です。
同じようにして、「12月9日(月)〜12月10日(金)」までの5日間も計算してみると、標準偏差は 3,162円でした。前5日間の 16,733円とは大きな差です。
この標準偏差の見方についてカンタンに言うと。だいたいのデータが「平均値±標準偏差」のなかに収まるよね、になります。
「12月2日(月)〜12月6日(金)」までの5日間のデータであれば、平均値 40,000±16,733円のなかにだいたいのデータが収まる。
「12月9日(月)〜12月10日(金)」までの5日間のデータであれば、平均値 40,000±3,162円のなかにだいたいのデータが収まる。
標準偏差の値が大きい、ということは。それだけデータのバラツキ度合いが大きいことを示しています。標準偏差が大きい「12月2日(月)〜12月6日(金)」までの5日間のほうが、データはたしかにバラツキが大きい。
下は 10,000円から上は 60,000円までのバラツキがあります。
いっぽうの「12月9日(月)〜12月10日(金)」までの5日間は、下は 35,000円から上は 45,000円までとバラツキは小さい。これが、標準偏差の差になってあらわれているのです。
したがって、平均値だけを見て(あるいは中央値をあわせて見ても)、どちらも同じような5日間だと見ていると、データのバラツキを見落とすことになります。
具体例の場合、どちらの5日間も同じ従業員数でシフトを組んでいたとしたらどうでしょう?
バラツキが小さい「12月9日(月)〜12月10日(金)」の5日間であればよいかもしれませんが、バラツキが大きい「12月2日(月)〜12月6日(金)」の5日間だと、過剰人員の日があったかもしれないことが推測できます。
売上高が少ない=客数も少ない、だとすれば。売上高が少ない日の従業員数は減らしたシフトを組むのがベストです(コスト削減という点では)。
平均値だけでデータを見ていると、これに気づかず、今後もずっと同じ従業員数でシフトを組み続けることにもなりかねません。過剰人員、過剰人件費が続きます。
お店にとっては金銭的な損失ですし、従業員は休みがなかなか取れず、昨今話題の働き方改革にも影響することでしょう。
このあたりも、データ数が多くなるほど、データを見ているだけでは気が付きにくいところになります。AVERAGE関数を使うときには、あわせてSTDEV.P関数も使うようにするのがおすすめです。
まとめ
AVERAGE関数(平均値)には、「外れ値の影響を受ける」「バラツキが見えない」という欠点が潜んでいます。
その欠点を補うために、「MEDIAN」と「STDEV.P」の2つの関数をあわせて使うようにしましょう。

