データ分析のお役立ちツールとして、Excelの「基本統計量」の使い方と見方とをご紹介します。
データ分析なら、まずは「基本統計量」で。
あるデータについて、その「特性」を知りたい。あるいは、知ることができたなら。と、考えることはありませんか?
たとえば。飲食店のオーナーが、「日別の来客数」というデータを持っていたとして。平均来客数や最多来客数など、そのデータが持つ特性を知りたい…
そんなときのお役立ちツールとして、Excelの分析ツール「基本統計量」というものがあります。
基本統計量は、「使い方」はとてもお手軽であるいっぽう、「見方」には少々の知識が必要です。というわけで、使い方と見方を身につけて、せっかくのデータを活かしましょう ↓
- これはカンタン!基本統計量の使い方
- コツさえつかめば!基本統計量の見方
それでは、このあと順番に見ていきます。
これはカンタン!基本統計量の使い方
まずは、基本統計量の「使い方」からお話をしていきます。
はじめて基本統計量の機能を使う場合には、Excelで「アドインの設定」が必要です。と言っても、難しくはありませんのでご安心を。
アドインの設定
まずは、Excelで「オプション」の画面を開きましょう。
「ファイル」タブを選択したあと、画面左下の「オプション」を選択する、のもよいですが。キーボードで、「Alt」「 T」「O」の順に押すだけのショートカットもおすすめです。
オプション画面が開いたら、左端のメニューのなかから「アドイン」を選択します ↓
続いて、Excelアドインの「設定」ボタンを押します ↓
すると、アドインの設定画面が開くので、「分析ツール」にチェックを入れて、「OK」ボタンを押しましょう ↓
これで、はじめの設定はおしまい。基本統計量の機能が使えるようになります。
基本統計量の使い方
それでは、いよいよ「基本統計量」を使ってみましょう。
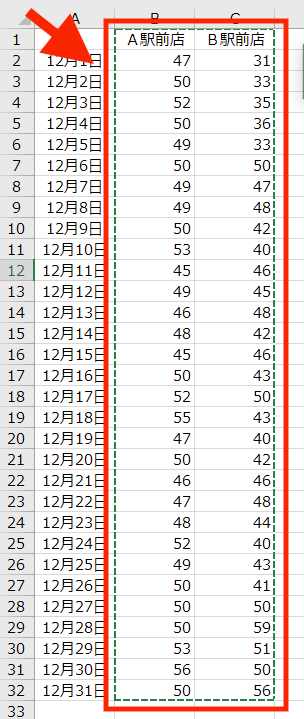
サンプルデータとして、とある飲食店の日別来客数のデータ(20XX年12月分)を用意しました。A駅前店とB駅前店、2店舗分のデータです ↓
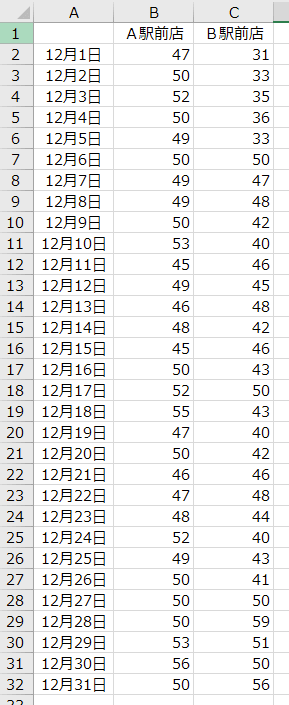
平日も土日も無休で営業する「繁忙」ぶりには目をつぶるとして。12月の1ヶ月分、つまり 31日分のデータです。
この数字(日別来客数)の羅列を見ても、なかなかデータの「特性」はわからないことでしょう。というわけで、「基本統計量」の出番になります。
「データ」タブのなかにある「分析」グループから、「データ分析」を選択しましょう ↓

データ分析のウィンドウが開くので「基本統計量」を選択して、「OK」ボタンを押します ↓
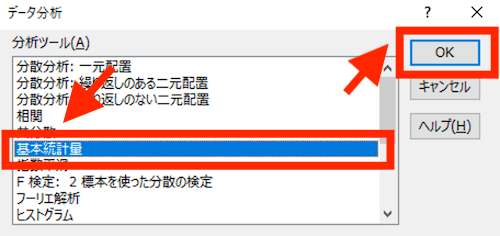
基本統計量のウィンドウが開くので、以下のように設定したあと「OK」ボタンをクリックします ↓
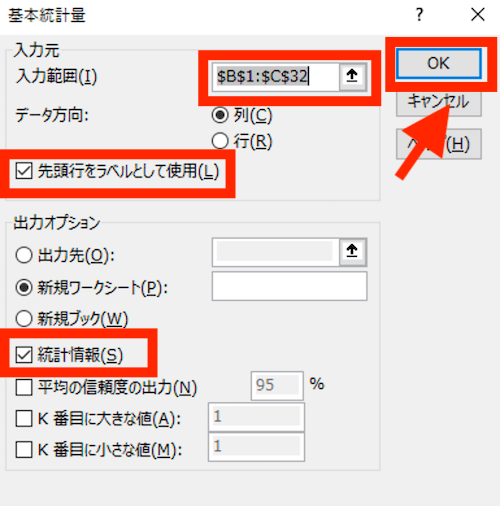
上記を設定するときのポイントは、「入力範囲」は先頭行を含めて、来店客数の値が入力されているセルを選択します(日付の列は含めません) ↓
「先頭行」とは、サンプルデータで言うと、「A駅前店」「B駅前店」と入力されている行です。そのうえで、「先頭行をラベルとして使用」にチェックを入れます。
なお、今回は2店舗のデータを使いましたが、1店舗だけでも、あるいは5店舗でも10店舗でも基本統計量は使えます。
加えて、「統計情報(S)」にチェックを入れるのを忘れずに。これで、基本統計量の結果が、あたらしいシートに表示されます ↓
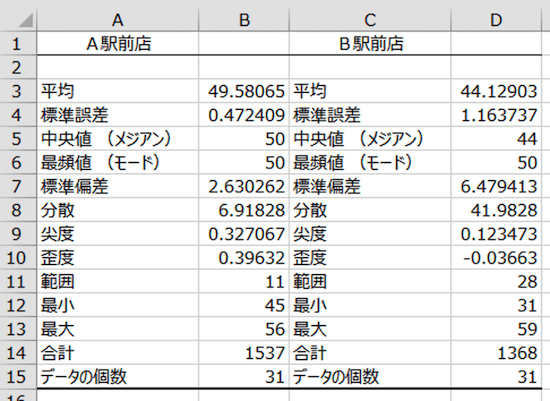
初めて見ると、「うげっ… なんじゃこりゃ」といった感じですから。このあと、基本統計量の見方についてお話をしていきます。
コツさえつかめば!基本統計量の見方
基本統計量の結果について、各項目の見方を順番に見ていきましょう。
平均
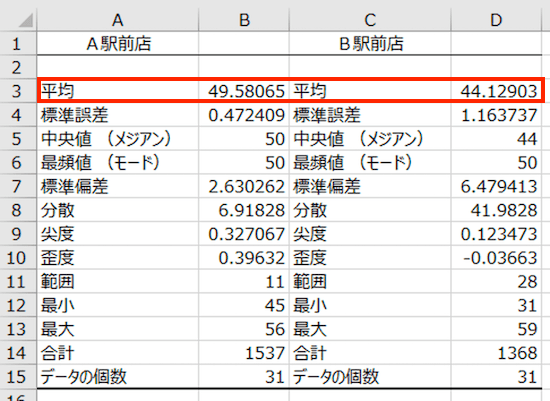
文字どおり、「平均」の値です。A駅前店、B駅前店それぞれの平均来客数が計算されています。
これを見ると。A駅前店のほうがB駅前店よりも、1日あたり来客数は5人強多いことがわかります(49.58065 − 44.12903)。
この「平均」をアタマに入れつつ、次の項目を見ていきましょう。
標準誤差
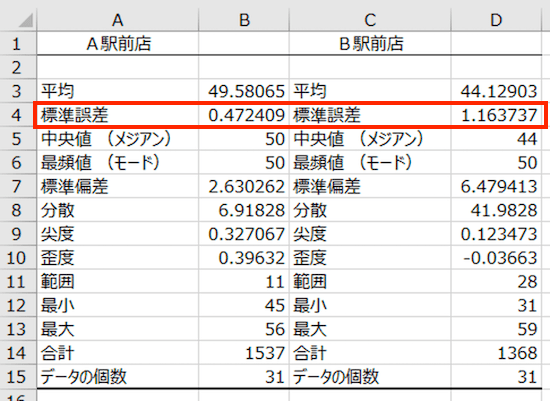
標準誤差とは、「平均の精度」を見る指標です。
A駅前店の平均は、さきほど「49.58065」であることを確認しました。ところが、この平均は 31日間という限られたデータの平均値です。
もしも、もっとたくさんのデータがあったなら、その「平均」はどのくらい変わってしまう可能性があるか? その答えがこちらです ↓
平均 49.58065 ± 標準誤差 0.472409。つまり、平均はだいたい 49〜50人くらいのあいだに落ち着くのではないか、ということになります。
いっぽうのB駅前店の場合には、標準誤差が「1.163737」と、A駅前店よりもだいぶ大きい。A駅前店の平均よりも誤差が大きい、という見方になります。
中央値
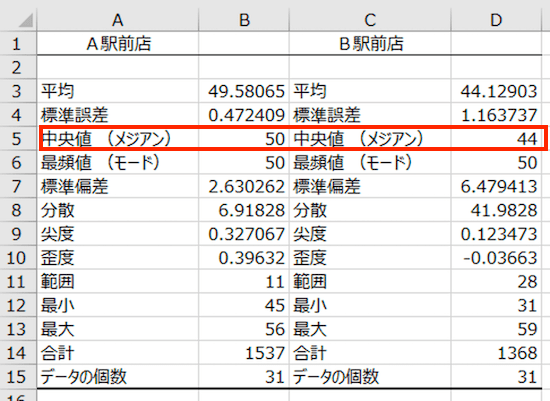
中央値とは、データを小さい順(あるいは大きい順)に並べたときに、ちょうど真ん中にあるデータの値のこと。もしも、データの個数が偶数であれば、真ん中の2つのデータの平均値になります。
中央値は、さきほどの「平均」と比較をしてみましょう。「平均よりも大きく外れている数値(外れ値と呼びます)」があると、平均と中央値とは乖離するからです。
平均と中央値とが乖離している場合には、平均は外れ値の影響を受けていることを考慮しなければいけません。
同じ平均の「50人」だとしても、31日間のほとんど毎日 50人のケースもあれば、ほとんどの日は20人くらいでたまに 100人の日があるというケースもあります。
前者は平均と中央値が同じくらいですが、後者は平均よりも中央値が小さくなるはずです。
A駅前店とB駅前店は、それぞれ平均と中央値が同じくらいであることから、「あまり外れ値はないのかなぁ」との見方になります。
最頻値
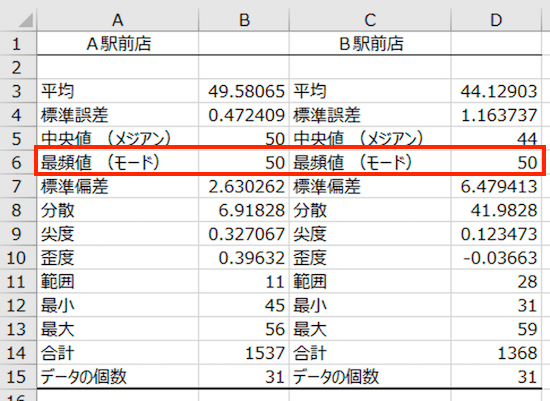
最頻値は、文字どおり「もっとも頻出する値」です。A駅前店もB駅前店も、50人の日がいちばん多かった、ということがわかります。
ところで。ここまで見てきた「平均」「中央値」「最頻値」には、ある共通点があります。それは「データの重心がどこにあるか?」をあらわしているということ。
まず、「平均」は、すべての値をならしたときの「重心」を示しています。
「中央値」は、順番に並べたときの真ん中であるという意味での「重心」を。「最頻値」は、もっとも頻出する値であるという意味での「重心」を示しています。
データにどのような偏りがあるか、データの重心はどこにあるか。平均、中央値、最頻値の意味を考えながら見るようにしましょう。
標準偏差、分散
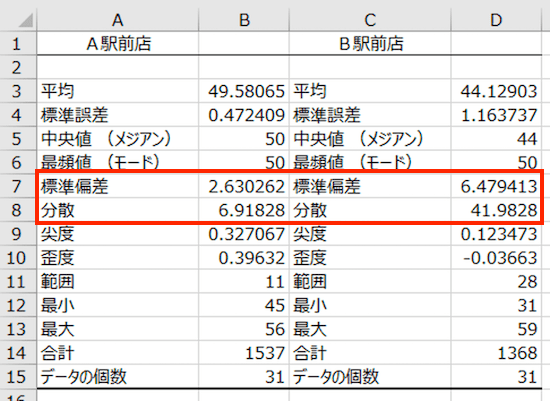
標準偏差とは、「データのばらつき」をあらわす指標です。
標準偏差に関するくわしい解説は省きつつ、ざっくり言うと。「平均 ± 標準偏差」のあいだに、だいたいのデータがおさまる、ということです。
A駅前店で言えば、「平均 49.58065 ± 標準偏差 2.630262」のあいだに、だいたいのデータ(12月31日間の毎日の来客数)がおさまることをあらわしています。
これに対して、B駅前店の標準偏差はA駅前店よりも大きく。日によって来客数に差がありそうだなぁ、といった見方ができそうです。
このあたりの確認は「標準偏差÷平均値(%)」を計算してみるのもよいでしょう。つまり、平均値に対する標準偏差の大きさはどのくらいか。
平均値の大きさに差がある場合には、単純に標準偏差の大小を比較するだけではわからないからですね。
というわけで、「標準偏差÷平均値(%)」の計算によれば。A駅前店は 5.3%、B駅前店は14.7%になります。やっぱり、A駅前店よりもB駅前店のほうが、毎日の来客数にばらつきが大きいようです。
B駅前店の店長は、いろいろな意味でオペレーションがたいへんそうだ… と、いったところでしょうか。
なお、「分散」とは。算式で言うと、「標準偏差の二乗」です。分散は、標準偏差を計算する過程で必要になるものであり、「分散」自体を見てなにかを考えることはないだろう。ということで、以上とします。
尖度、歪度
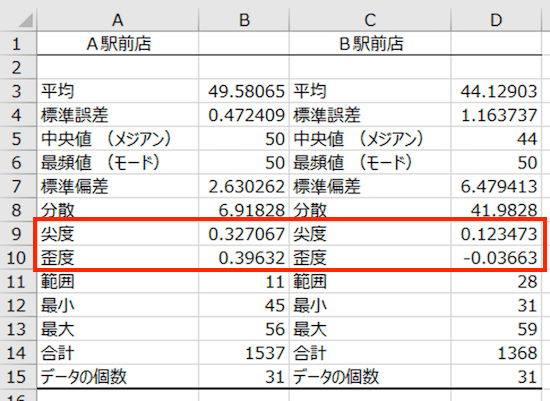
尖度と歪度は、データがどのように分布しているかをあらわす指標です。
そんな「尖度」と「歪度」を理解するにあたっては、「正規分布」を知っておかねばなりません。正規分布をイメージであらわすと、こんな感じです ↓
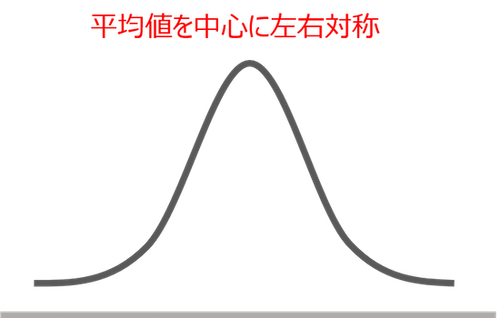
日別の来客数のデータを頻度に応じて並べた場合に、「平均」の値を中心にして左右対称にきれいに分布すれば、上図のようになります。
では、A駅前店とB駅前店の場合はどうなのか? と言えば、こちらです ↓
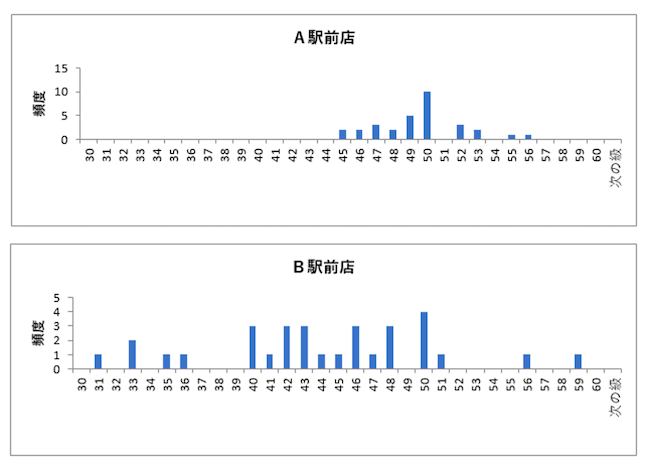
さきほどの正規分布に比べると、全然きれいに分布していません。このような「正規分布との違い」を数値であらわすのが、「尖度」と「歪度」です。
まず、尖度の見方はこのとおり ↓
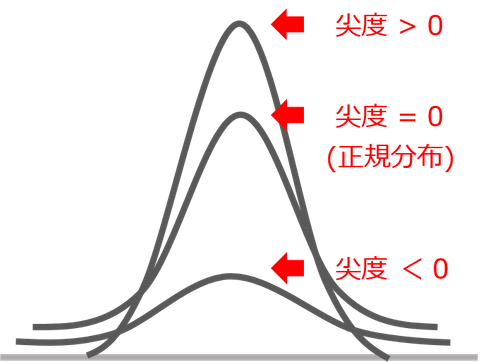
上図のとおり、正規分布が「尖度 = 0」として。正規分布より山が尖るほど「尖度 > 0」、山がなだらかになるほど「尖度 < 0」です。
いっぽうの「歪度」は、このとおり↓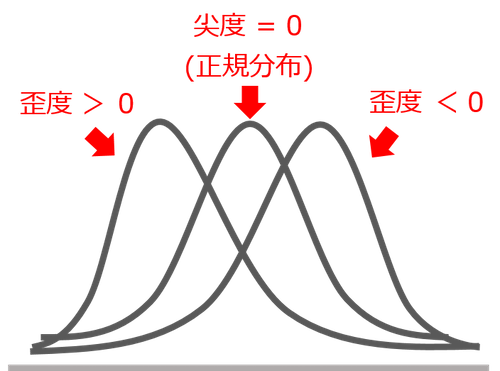
上図のとおり、正規分布が「歪度 = 0」として。正規分布より山が右にかたよるほど「歪度 < 0」、山が左にかたよるほど「歪度 > 0」です。
あらためて、A駅前店とB駅前店の尖度と歪度を見てみると ↓

A駅前店のほうがB駅前店よりも山が尖っていて(尖度が大きい)、その山が左に偏っている(歪度が大きい)ことがわかります。
逆に、B駅前店はA駅前店よりも山がなだらかで(尖度が小さい)、その山に偏りはほとんどありません(歪度が小さい)。そのようすを再掲して確認してみましょう ↓

このように、尖度と歪度がわかれば、「データがどのように分布しているか」をイメージできるのです。
範囲・最小・最大・合計・データの個数
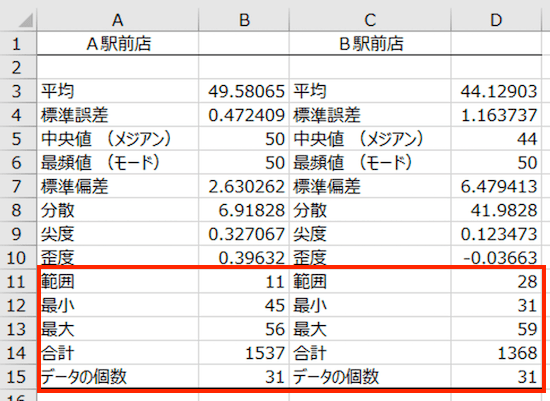
残りの項目は、それほどの説明を要しない部分です。
まず「最小」は、データのうち最小の値。「最大」はデータのうち最大の値です。「範囲」はその「最小」と「最大」の差になります。
つまり、「範囲」はどれくらいのエリアにデータが散らばっているかをあらわしているわけです。
「合計」は、文字どおり、すべてのデータの合計値です。今回の場合には、31日間の来客数の合計になります。
「データの個数」も文字どおり。今回の場合には、31日間のデータですから、31個ということになります。
前述した「平均」は、「合計 ÷ データの個数」で計算されていることも確認をしておきましょう。
まとめ
あるデータの特性を知るためのお役立ちツールとして、Excelの「基本統計量」についてお話をしてきました。
基本統計量の結果は、代わりに関数で計算をしたり、グラフを作成したりもできますが。基本統計量は、使い方がお手軽であるうえに、豊富な情報を得られるところにメリットがあります。
ぜひ、使い方と見方を押さえておきましょう。

